The Relationship Between Covariance and Dot Product
Covariance and the dot product are related concepts in mathematics and statistics, particularly in the context of vectors and random variables. Here's how they are connected:
Dot Product
The dot product (also known as the scalar product) of two vectors a and b in n-dimensional space is given by:
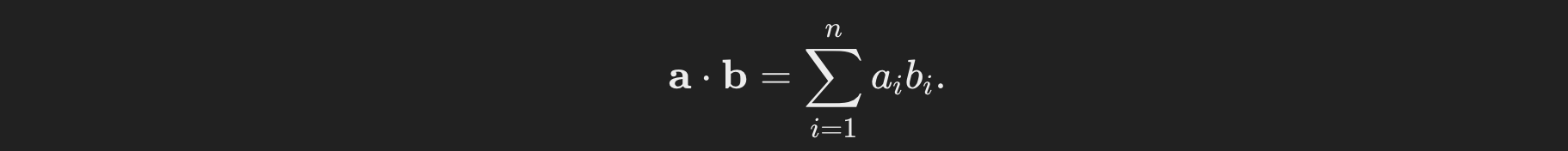
This operation results in a single scalar value and provides a measure of the similarity between the two vectors. If the vectors point in the same direction, the dot product is positive and large; if they point in opposite directions, the dot product is negative; if they are orthogonal, the dot product is zero.
Covariance
Covariance is a measure of how much two random variables X and Y change together. It is given by:
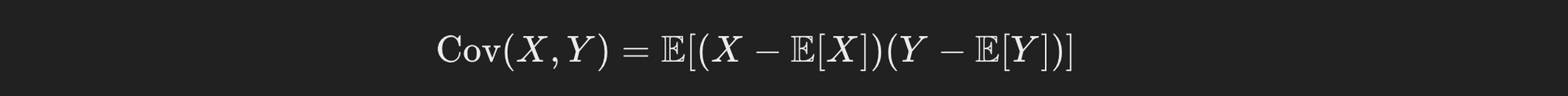
Where E denotes the expected value. If the covariance is positive, the variables tend to increase together; if it is negative, one tends to increase when the other decreases.
Relationship
The relationship between covariance and the dot product can be seen in the context of centered random variables. If you consider the centered random variables:
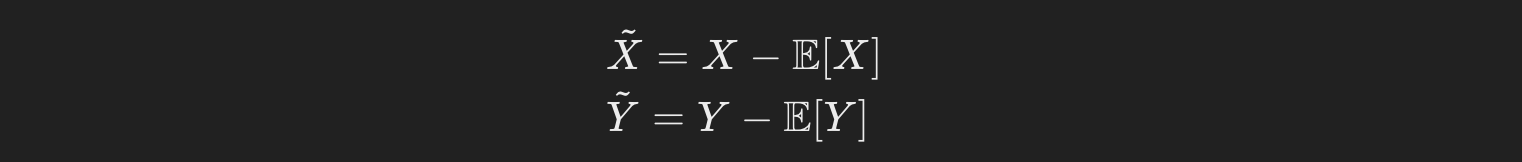
the covariance between X and Y can be interpreted as the dot product of these centered variables in the space of random variables, normalized by the number of observations n:
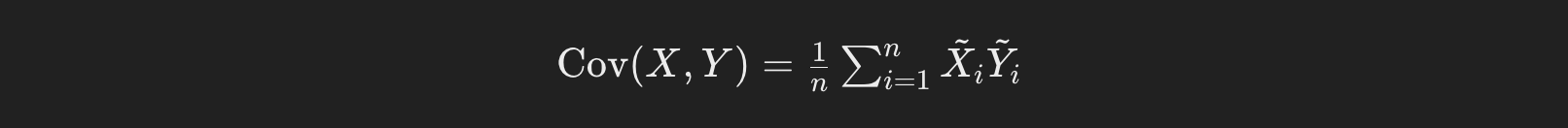
Here, tilde_X_i and tilde_Y_i are the deviations from the mean of the random variables X and Yrespectively. This sum is analogous to the dot product, where the sum of the products of corresponding elements gives a measure of the overall relationship between the two sets of values.
Summary
In summary, covariance can be viewed as a normalized dot product of centered random variables. Both operations measure how two sets of values relate to each other, with the dot product being a geometric measure in vector space and covariance being a statistical measure in the space of random variables.